This template will return the correlation matrix of supplied numerical variables.
Correlation is one of the most commonly used statistical tool. With the help of that we can get information about a possible linear relation between two variables. According to the definition of the correlation, one can call it also as the standardized covariance.
The maximum possible value of the correlation (the so-called correlation coefficient) could be 1, the minimum could be -1. In the first case there is a perfect positive (thus in the second case there is a perfect negative) linear relationship between the two variables, though perfect relationships, especially in the social sciences, are quite rare. If two variables are independent from each other, the correlation between them is 0, but 0 correlation coefficient only means certainly a linear independency.
Because extreme values occur seldom we have rule of thumbs for the coefficients, like other fields of statistics:
Please note that correlation has nothing to do with causal models, it only shows association but not effects.
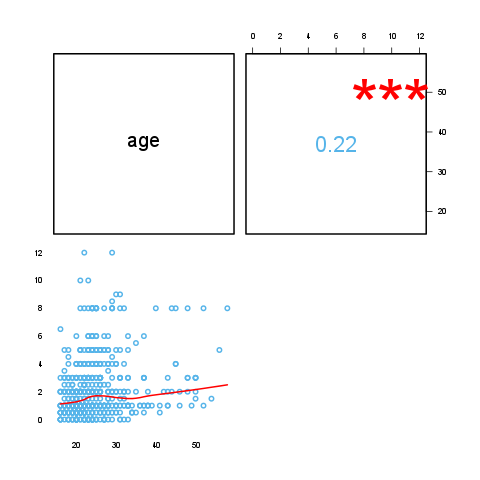
709 variables with 2 cases provided.
There are no highly correlated (r < -0.7 or r > 0.7) variables.
There are no uncorrelated correlated (r < -0.2 or r > 0.2) variables.
| age | edu | |
|---|---|---|
| age | 0.2185 * * * | |
| edu | 0.2185 * * * |
Where the stars represent the significance levels of the bivariate correlation coefficients: one star for a p value below 0.05, two for below 0.01 and three for below 0.001.
On the plot one can see the correlation in two forms: below the diagonal visually, above that one can find the coefficient(s).
This template will return the correlation matrix of supplied numerical variables.
Correlation is one of the most commonly used statistical tool. With the help of that we can get information about a possible linear relation between two variables. According to the definition of the correlation, one can call it also as the standardized covariance.
The maximum possible value of the correlation (the so-called correlation coefficient) could be 1, the minimum could be -1. In the first case there is a perfect positive (thus in the second case there is a perfect negative) linear relationship between the two variables, though perfect relationships, especially in the social sciences, are quite rare. If two variables are independent from each other, the correlation between them is 0, but 0 correlation coefficient only means certainly a linear independency.
Because extreme values occur seldom we have rule of thumbs for the coefficients, like other fields of statistics:
Please note that correlation has nothing to do with causal models, it only shows association but not effects.
709 variables with 3 cases provided.
The highest correlation coefficient (0.2273) is between edu and age and the lowest (-0.03377) is between leisure and age. It seems that the strongest association (r=0.2273) is between edu and age.
There are no highly correlated (r < -0.7 or r > 0.7) variables.
Uncorrelated (-0.2 < r < 0.2) variables:
| age | edu | leisure | |
|---|---|---|---|
| age | 0.2273 * * * | -0.0338 | |
| edu | 0.2273 * * * | 0.1732 * * * | |
| leisure | -0.0338 | 0.1732 * * * |
Where the stars represent the significance levels of the bivariate correlation coefficients: one star for a p value below 0.05, two for below 0.01 and three for below 0.001.
On the plot one can see the correlation in two forms: below the diagonal visually, above that one can find the coefficient(s).
This template will return the correlation matrix of supplied numerical variables.
Correlation is one of the most commonly used statistical tool. With the help of that we can get information about a possible linear relation between two variables. According to the definition of the correlation, one can call it also as the standardized covariance.
The maximum possible value of the correlation (the so-called correlation coefficient) could be 1, the minimum could be -1. In the first case there is a perfect positive (thus in the second case there is a perfect negative) linear relationship between the two variables, though perfect relationships, especially in the social sciences, are quite rare. If two variables are independent from each other, the correlation between them is 0, but 0 correlation coefficient only means certainly a linear independency.
Because extreme values occur seldom we have rule of thumbs for the coefficients, like other fields of statistics:
Please note that correlation has nothing to do with causal models, it only shows association but not effects.
32 variables with 11 cases provided.
The highest correlation coefficient (0.902) is between disp and cyl and the lowest (-0.8677) is between wt and mpg. It seems that the strongest association (r=0.902) is between disp and cyl.
Highly correlated (r < -0.7 or r > 0.7) variables:
Uncorrelated (-0.2 < r < 0.2) variables:
| mpg | cyl | disp | |
|---|---|---|---|
| mpg | -0.8522 * * * | -0.8476 * * * | |
| cyl | -0.8522 * * * | 0.9020 * * * | |
| disp | -0.8476 * * * | 0.9020 * * * | |
| hp | -0.7762 * * * | 0.8324 * * * | 0.7909 * * * |
| drat | 0.6812 * * * | -0.6999 * * * | -0.7102 * * * |
| wt | -0.8677 * * * | 0.7825 * * * | 0.8880 * * * |
| qsec | 0.4187 * | -0.5912 * * * | -0.4337 * |
| vs | 0.6640 * * * | -0.8108 * * * | -0.7104 * * * |
| am | 0.5998 * * * | -0.5226 * * | -0.5912 * * * |
| gear | 0.4803 * * | -0.4927 * * | -0.5556 * * * |
| carb | -0.5509 * * | 0.5270 * * | 0.3950 * |
| hp | drat | wt | |
|---|---|---|---|
| mpg | -0.7762 * * * | 0.6812 * * * | -0.8677 * * * |
| cyl | 0.8324 * * * | -0.6999 * * * | 0.7825 * * * |
| disp | 0.7909 * * * | -0.7102 * * * | 0.8880 * * * |
| hp | -0.4488 * * | 0.6587 * * * | |
| drat | -0.4488 * * | -0.7124 * * * | |
| wt | 0.6587 * * * | -0.7124 * * * | |
| qsec | -0.7082 * * * | 0.0912 | -0.1747 |
| vs | -0.7231 * * * | 0.4403 * | -0.5549 * * * |
| am | -0.2432 | 0.7127 * * * | -0.6925 * * * |
| gear | -0.1257 | 0.6996 * * * | -0.5833 * * * |
| carb | 0.7498 * * * | -0.0908 | 0.4276 * |
| qsec | vs | am | |
|---|---|---|---|
| mpg | 0.4187 * | 0.6640 * * * | 0.5998 * * * |
| cyl | -0.5912 * * * | -0.8108 * * * | -0.5226 * * |
| disp | -0.4337 * | -0.7104 * * * | -0.5912 * * * |
| hp | -0.7082 * * * | -0.7231 * * * | -0.2432 |
| drat | 0.0912 | 0.4403 * | 0.7127 * * * |
| wt | -0.1747 | -0.5549 * * * | -0.6925 * * * |
| qsec | 0.7445 * * * | -0.2299 | |
| vs | 0.7445 * * * | 0.1683 | |
| am | -0.2299 | 0.1683 | |
| gear | -0.2127 | 0.2060 | 0.7941 * * * |
| carb | -0.6562 * * * | -0.5696 * * * | 0.0575 |
| gear | carb | |
|---|---|---|
| mpg | 0.4803 * * | -0.5509 * * |
| cyl | -0.4927 * * | 0.5270 * * |
| disp | -0.5556 * * * | 0.3950 * |
| hp | -0.1257 | 0.7498 * * * |
| drat | 0.6996 * * * | -0.0908 |
| wt | -0.5833 * * * | 0.4276 * |
| qsec | -0.2127 | -0.6562 * * * |
| vs | 0.2060 | -0.5696 * * * |
| am | 0.7941 * * * | 0.0575 |
| gear | 0.2741 | |
| carb | 0.2741 |
Where the stars represent the significance levels of the bivariate correlation coefficients: one star for a p value below 0.05, two for below 0.01 and three for below 0.001.
On the plot one can see the correlation in two forms: below the diagonal visually, above that one can find the coefficient(s).
This report was generated with R (3.0.1) and rapport (0.51) in 4.769 sec on x86_64-unknown-linux-gnu platform.
